In this post, I will argue that the ontological argument explains the existence of the fundamental law of physics, i.e., a Theory of Everything. So, this will be a reasonably satisfying solution to the fundamental question of metaphysics: Why is there anything at all? I will argue that the fundamental law of physics is a logically necessary entity, and after its existence is justified, all things physical will follow from it. The Theory of Everything is the only mathematical entity whose existence is uplifted into the physical reality.

• Introduction
• The argument
  • Spacetime
  • The only assumption
• Defining the greatness of a theory
  • Simplicity
  • Generality
  • Less number of fundamental dimensionless constants
  • Uniqueness
  • Predictive power
  • Reductionism
• Consciousness
• Problem of Evil
• Modal realism
• Rigour
• Criticism by Graham Oppy and my reply
• Conclusion

Note: I thought I had recently proposed this argument. But on 4th October 2021, I already posted this as a comment in a blog post by Aron Wall.

Introduction

I will try to make a nonrigorous argument just like the original one by Anselm of Canterbury. I will mention at the end about a possible rigorous version like Gödel’s ontological argument.

Even though I am an atheist, I have always found ontological arguments very fascinating. It seems like the only possible explanation for “Why is there anything at all?”

Many physicists, including Stephen Hawking, Lawrence Krauss, and Frank Wilczek, have moved the goalposts and answered a different (but still important) question.

“The answer to the ancient question “Why is there something rather than nothing?” would then be that ‘nothing’ is unstable.”

― Frank Wilczek

What they did is define the state with no particles in semiclassical gravity as “nothing”. Then, they try to argue that this “nothing” is a false vacuum and that this “nothing” decays to a true vacuum that contains particles. But what philosophers call “nothing” is very different. We can’t already assume the existence of these 2 things: 1) laws of physics (in their case, semiclassical gravity) and 2) spacetime. When philosophers say nothing, even these things are not allowed. They also didn’t work in quantum gravity but just in the semiclassical gravity approximation.

Let me quote Sean M. Carroll’s criticism of Wilczek, Hawking etc from his 1802.02231,

“Cosmological evolution plausibly involves a transition from a symmetric vacuum state, free of particles, to a collection of particles in a background given by a lower-energy vacuum. In some models, this evolution could dynamically favor matter over antimatter, helping to explain the current asymmetry in our observed universe. Such a scenario has given rise to the pithy saying that there is something rather than nothing because “nothing is unstable” [26, 27], if we allow ourselves the freedom to define “nothing” as “a symmetric false-vacuum state.” This has nothing at all to do with the origin of the universe itself, and certainly nothing to do with why there is a quantum wave function in the first place.

In the context of creation of something from nothing, we must also face the issue of “quantum fluctuations.” It is often said that the quantum vacuum is filled with fluctuating virtual particles, and even that these particles sometimes pop into real existence, as in Hawking radiation from black holes [29]. This is a misleading description, arising from a tendency to speak as if wave functions represent statistical ensembles of classical particles, rather than true quantum states. A quantum state is simply a quantum state, and a true vacuum state will be stationary, with nothing “fluctuating” at all. Hawking particles can be emitted by black holes because a state with a black hole is not the vacuum state, and the wave function of a black hole state naturally evolves into one with particles radiating away as the black hole shrinks.”

― Sean M. Carroll

But in that paper Carroll was pessimistic that an explanation is possible and took the brute fact approach similar to Bertrand Russell.

But what those physicists have tried to answer is also an important question. They tried to explain all physics given the existence of laws of physics and spacetime. The only caveat is that gravity is classical in their approach. Some people like David Albert think these vacuum states are just as particular as a giraffe. This is nonsense. A giraffe has a biological structure: its body shape, digestive track shape, skeleton, DNA, etc. If you zoom in more, you will see a giraffe’s chemical structure containing many organic materials. If you zoom further, you will reach a point where classical mechanics describes it. If you keep zooming, you will see scales where quantum mechanics and then QFT are applicable. Finally, when the giraffe is zoomed to near the Planck scale, you will see quantum spacetime where quantum gravity is applicable. All physical phenomena supervene on the fundamental laws of physics. So, a giraffe is much more complicated than a fundamental physics theory. Our ideas of things like giraffes are very approximate descriptions of emergent entities. For example, even water doesn’t exist fundamentally, but only approximately. You can’t assume that water/giraffe exists without assuming quantum fields exist. In the pecking order of ontological commitment, quantum fields are much higher than water/giraffes.

“Relativistic-quantum-field-theoretical vacuum states—no less than giraffes or refrigerators or solar systems—are particular arrangements of elementary physical stuff. The true relativistic-quantum-field-theoretical equivalent to there not being any physical stuff at all isn’t this or that particular arrangement of the fields—what it is (obviously, and ineluctably, and on the contrary) is the simple absence of the fields.”

― David Albert

References:

1. Ontological arguments - plato.stanford.edu by Graham Oppy, Joshua Rasmussen, & Joseph Schmid
2. Ontological argument - Wikipedia
3. Ontological argument - RationalWiki
4. Graham Oppy’s Ontological Arguments and Belief in God (1996 book) amazon or philpapers.org

I only read the first 3. From 2021, I wanted to read Graham Oppy’s (“the most formidable defender of atheism living today”) book but never got time.

“Superstring Theory and its non-perturbative completions (M- and F-theory) enjoy a unique status in the twin realms of physical theories and mathematical constructs. It may be argued that it is the universal entity in both realms. For this reason, Superstring Theory is also known as the Theory of Everything (TOE).

…

“Rigidity” of Quantum Gravity, and the overdetermined nature of its consistency requirements, suggest that there are just a “few” distinct solutions to the conditions, that is, only a “few” consistent theories of Quantum Gravity each of which is rigid, i.e. without adjustable parameters. There is a widespread belief that only finitely many quantum gravities exist (albeit “phenomenologically” their number may look huge).

This entails that string theories provide a finite fraction of all quantum gravities. It may even be true that they exhaust the full class. Even if this is not the case, given the restrictiveness of the consistency conditions, one expects that there are “not many more” consistent quantum gravities and that all consistent models “look roughly like string theory” since they should realize the same “implausible” miracles. This idea is a (conjectural) physical principle called the “String Lamppost Principle” (SLP).” [From the 2023 textbook “Introduction to String Theory”]

― Sergio Cecotti

The argument

The below argument from 1. to 9. argues there is an entity whose physical existence is logically necessary without using any information about physical reality. That means you cannot imagine a consistent physical reality where this entity doesn’t exist and it must physically exist a priori without any physical reason. This entity is the Theory of Everything (ToE) that governs all physical phenomena. It is most likely string/M-theory¹ but I will just use ToE as a placeholder name.

Note that even before we know the existence of any physical entity, we know that mathematics exists in the Platonic sense. This is called Mathematical Platonism (1,2,3). There are critics of Mathematical Platonism who think mathematics only exists inside the imaginations of humans, but I think when you look into a zoom video of the Mandelbrot set it should convince you that mathematics is not man-made. Furthermore, once the existence of the physical world is known, we can use the Quine–Putnam indispensability argument (1,2,3) to go back and argue for the existence of the Mathematical Platonic realm, but I can’t use that because I am using the existence of the Mathematical Platonic realm to explain the existence of the physical world.

1. Assume ToE does not exist physically.
2. “ToE” is defined as “the greatest entity in the Mathematical Platonic Realm”. (definition)
3. “The greatest entity in the Mathematical Platonic Realm” must, therefore, not exist physically and exist only Platonically. (from 1 & 2).
4. If “the greatest entity in the Mathematical Platonic Realm” were to exist in physical reality as well as in Platonic Mathematics, it would be even “greater”. (assumption or premise)
5. But that would mean “the greatest entity in the Mathematical Platonic Realm” is not actually the “greatest” entity in the Mathematical Platonic Realm since it could be even “greater”. (from 3 & 4).
6. “The greatest entity in the Mathematical Platonic Realm” must exist in both Platonic Mathematics and also in physical reality for it to be the “greatest” entity in the Mathematical Platonic Realm.
7. Therefore 1 & 2 are inconsistent.
8. Premise 1 cannot be true since 2 is just a definition (reductio ad absurdum).
9. Therefore, the ToE exists in physical reality.

So, our conclusion is that the Theory of Everything (ToE) must exist in physical reality for purely logical reasons without any physical reason.

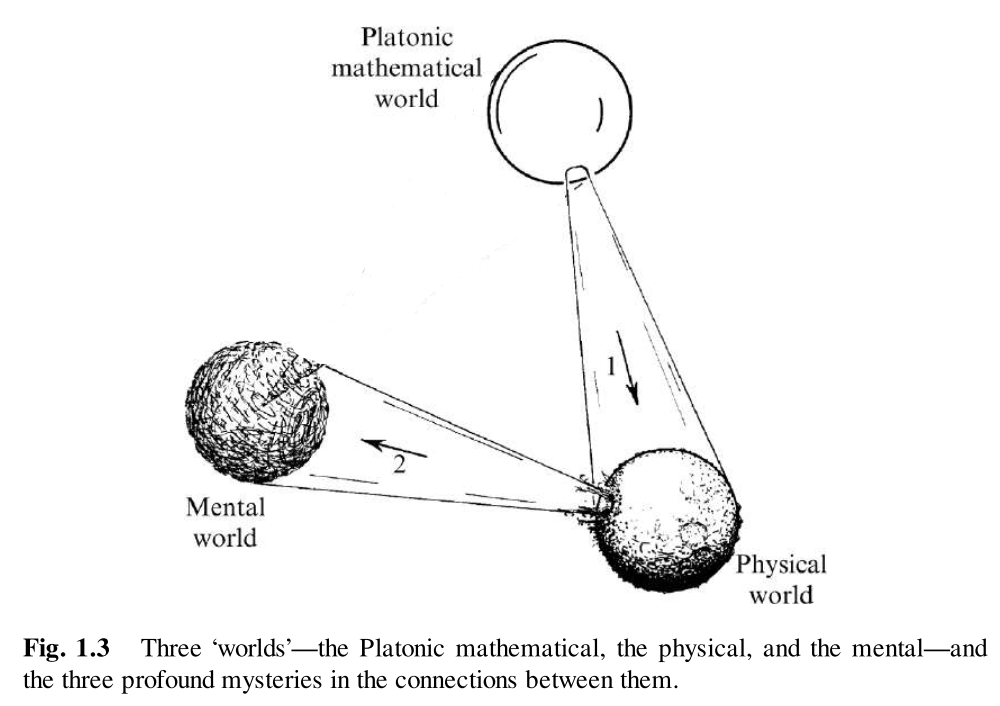
In the above Fig. 1.3 from The Road to Reality, Penrose talks about the “three worlds”. What I believe is very similar except I removed the connection between the mental world and the Platonic mathematical world in his image. I believe that the physical world inherently depends on the Platonic mathematical world. Similarly, the mental world (which contains things like moral truths, colours, anger, love, etc) inherently depends on the physical world (and also the Platonic mathematical world). But the Platonic mathematical world doesn’t depend on anything else.

This post is very much in the spirit of pantheism, but it will be counterproductive to use the word “God” for an equation because, in religions, it is always used to mean a anthropomorphic god who thinks exactly like a tribalistic, immoral, primitive Bronze Age man. Such a word will only tarnish the greatness of the laws of physics and should be considered pejorative. Einstein’s biggest blunder was not the cosmological constant incident but calling the laws of physics as God. Now, most people think he believed in a traditional anthropomorphic God instead of pantheism.

Spacetime

What do I mean by “exist in physical reality”? If you think about some number like 5 (or any other mathematical entity except the ToE), it exists in the abstract Platonic sense and you can’t locate it at some point in spacetime. But the Theory of Everything (ToE) is different because it is omnipresent. It must exist everywhere in spacetime and enforce itself on every physical phenomena. This is the only such mathematical equation that exists in the physical reality.

Once we have justified the physical existence of the ToE, then the existence of spacetime follows from it. For example, if the ToE is string/M-theory, then it demands an 11D quantum spacetime as it is the only type of spacetime where it can exist. After we have justified the existence of the ToE and spacetime, the existence of all things physical will follow from these 2.

The only assumption

The only assumption is 4. To me, it seems very obvious that an equation would become greater by existing in physical reality. Also, the ToE is the only mathematical entity that exists in physical reality. I mean, such a unique chance to uplift its existence from mathematical to both physical and mathematical among the infinite mathematical entities should obviously increase an entity’s greatness.

“In philosophy, if you think the answer is obvious, you haven’t understood the question.” [Twitter]

― Keith Frankish

Defining the greatness of a theory

Traditionally, when theists use the ontological argument for the existence of their fictional god, they generally do not properly define what they mean by “greatness”. In our context, we can say much more about it.

Simplicity

The ToE will be an equation that can probably fit into a SINGLE paper. That means it can be COMPLETELY specified with very little information. Simplicity is an expected property of the ToE. General Relativity can explain everything about classical gravity without the need for Horndeski’s theory, which is the most general classical gravity theory. General Relativity is, therefore, greater than Horndeski’s theory. In Horndeski’s theory, G2 to G5 are arbitrary functions. So, it is definitely not simple.

If you look at ANY good theory like General Relativity long enough, it will look trivial because of the metaphysical simplicity of fundamental physics. Another example is AdS/CFT, which looks obvious once we realize that local observables in dynamical spacetime theories are not diffeomorphism invariant, and therefore, all observables are forced to exist at the boundary (like S-matrix in flat space). The nontrivial part is that these AdS boundary conditions behave like a well-defined local CFT.

MOND and Bohmian mechanics are examples of fake simplicity. If we make them relativistic, they become complicated.

If there is a necessary entity, Occam’s razor also suggests us that it would be something simple like an equation rather than a complicated being. If someone wants to COMPLETELY specify everything about the Abrahamic god it will be impossible. Divine Simplicity is one of the most illogical ideas coming out of Abrahamic theology. Any God of any religion has many properties. For example, most gods have a preferred language, like Sanskrit for Hindu gods, Hebrew for Yahweh, and Arabic for Allah. Most gods also have some sort of chosen people, like Brahmins for Hindu gods. Most religions also have very specific rituals that must be done so that their god doesn’t hate them and torture them in the afterlife. You can’t deduce these things from something simple like an equation. In principle, all the 100s of pages of information in their holy books/scriptures is necessary (but not sufficient) to uniquely define such a god. These books are not sufficient because the moral laws given in such books (presumably what these gods follow) are very vague and when such a god is faced with problems that are more complicated than the trolley problem, these rules do not tell what these gods will do. So, a God is never a simple answer to the question.

Generality

Any theory that is a particular limit of another theory is less great than the more general theory if the more general theory introduces new physical concepts.

For example, General Relativity is greater than Special Relativity because Special Relativity is a specific limit of it. We should take the limit where spacetime becomes nondynamical Minkowski spacetime to get Special Relativity.

If we again consider General Relativity vs Horndeski’s theory, you might say that, unlike last time, this time, Horndeski’s theory is better because it contains GR as a limit. But I think it is a fake generality. It doesn’t make any new conceptual leaps. General Relativity taught us that the spacetime is dynamic. Horndeski’s theory uses the same mathematical tools and the same physical concepts. We can always add a fake parameter that can be taken to zero to get back our theory. That doesn’t mean we got a proper, more general theory.

String/M-theory is a more general theory than General Relativity, and unlike Horndeski’s theory, it actually introduces many new physical concepts. So, it is greater than General Relativity.

Less number of fundamental dimensionless constants

We don’t know any explanation for why fundamental dimensionless constants are what they are. So, the less they are, the greater the theory. Ideally 0. The Standard Model requires 25 fundamental dimensionless constants.

Again, let’s compare General Relativity vs Horndeski’s theory. The former has no fundamental dimensionless constants, and the latter has many arbitrary functions whose Taylor expansion contains many fundamental dimensionless constants.

Perturbative string theory has only 1 fundamental dimensionless constant, the string length in the Planck units (the string coupling constant is also a fundamental dimensionless constant, but it is not independent. One of these 2 will automatically give the other. When we say small coupling constant, it means the same as large string length in the Planck units). But M-theory (non-perturbative string theory) has no fundamental dimensionless constant, just like GR. The string coupling and the string length are given by \(g_{\mathrm{s}}=\left(\dfrac{R_{11}}{\ell_{P}}\right)^{3 / 2}\quad \text{and}\quad\ell_{s}=\ell_{P}\left(\dfrac{R_{11}}{\ell_{P}}\right)^{-1 / 2}\) where $\ell_{P}$ is the 11D Plack length and $R_{11}$ is the radius of the dimension that we compactify to get type IIA string theory.

Uniqueness

One of the biggest problems of religions is the utter lack of any uniqueness. When a theist uses an argument like the ontological argument or the Kalam cosmological argument etc, they merely argue for the existence of something. They don’t even argue that this thing has consciousness. Even if we do agree with them that their argument implies a anthropomorphic conscious God, they will still have tens of thousands of Gods dreamed by humans. They never argue about picking the right one among them. They answer to this depends very illogically on the geography of a theist. A theist will say that these arguments point towards the existence of Christian God or Brahman or Allah based on whether they are born in the West or India or the middle east.

But the laws of physics are highly unique. Theories like General Relativity are already unique if you demand the simplest classical theory of dynamical spacetime. String theory takes uniqueness to the next level. There are only 5 perturbative string theories. All of them are secretly dual to each other and are specific limits of the unique M-theory. Unlike in General Relativity, here we do not even need to demand the simplest theory to achieve uniqueness.

Predictive power

The ToE will predict any physical phenomena to an arbitrarily high precision. We have never seen anything like that in the history of science before. Until now, we have only seen effective theories that only work until some UV cutoff.

Compare this again with religion. Religions never make any proper predictions. They make false claims about the afterlife that are already falsified. Recall that when a part of your brain is damaged by accident etc, you will forget some things. The more severe the damage, the more things you will forget. So, it should be clear that when a person dies and microorganisms eat their brain, then that person’s consciousness is completely gone. But religions believe that in your afterlife, you will have all of your memories and all of your cognitive capacity even after microorganisms completely eat your brain. That is an extraordinary claim that requires extraordinary evidence. But theists provide zero evidence for the afterlife.

Reductionism

Reductionism is inbuilt into the laws of physics. This allows us to start at some scale that we can probe and understand. Then, we can move to smaller and smaller scales. This is the philosophy behind the effective field theory approach.

“It is a basic fact of life that Nature comes to us in many scales. Galaxies, planets, aardvarks, molecules, atoms and nuclei are very different sizes, and are held together with very different binding energies. Happily enough, it is another fact of life that we don’t need to understand what is going on at all scales at once in order to figure out how Nature works at a particular scale. Like good musicians, good physicists know which scales are relevant for which compositions.” [2007]

― C. P. Burgess

Theists also think everything that happens will happen because of their God, and he routinely violates the laws of physics to do miracles. But, the difference is in the case of the ToE; we already have a lot of evidence for reductionism because we humans have already greatly succeeded in reducing all physical phenomena into the General Relativity and Standard model. We are only missing the last step, where these 2 are unified. But no religion has made ANY progress in explaining EVERYTHING from their God. Once you have the ToE, then every physical phenomenon can be quantitatively explained from it. Let alone quantitative, no religion has even given qualitative explanations about why the universe is like this. Theists can’t deduce from their God’s definition when and what miracles he will do, etc.

They can’t start with the properties of their God and deduce all natural and supernatural phenomena from that. Reductionism is inconsistent with a God even though theists claim everything can be reduced to their God.

Consciousness

The ToE will not have consciousness. And that is a great property.

We have only ever seen consciousness in highly complicated biological entities. Consciousness emerges only when a large number of molecules are arranged in highly specific patterns. So, consciousness is inconsistent with the expected simplicity of the necessary entity. Consciousness is inconsistent with the Divine Simplicity. This is another reason the ToE is a better answer to the necessary entity than a conscious God.

There is another different criticism from existentialism about why God shouldn’t be conscious due to Sartre.

“For if God is consciousness, he is integrated in the totality. And if by his nature he is a being beyond consciousness (that is, an in-itself which would be its own foundation) still the totality can appear to him only as object (in that case he lacks the totality’s internal integration as the subjective effort to reapprehend the self) or as subject (then since God is not this subject, he can only experience it without knowing it). Thus no point of view on the totality is conceivable; the totality has no ‘outside’ and the very question of the meaning of the ‘underside’ is stripped of meaning. We cannot go further.” [p. 302 of Being and Nothingness. The translator Hazel E. Barnes explained in the preface that this para means “Again we can not without contradiction look on God as an intelligent being who both transcends and includes the totality.”]

― Jean-Paul Sartre

Problem of Evil

Religions that claim an omnipotent and omnibenevolent God will suffer from the problem of evil. If you are as powerful as Superman or Goku, then when you see someone getting murdered with a gun, you have a moral obligation to stop because you have no danger with a mere gun. Similarly, God is obligated to help everyone and ensure no evil ever happens.

Moral Agents: Only sapient beings (i.e., able to think abstractly) are moral agents. Nonsapient beings cannot be morally judged. Sentient nonhuman animals are, therefore, not moral agents. Similarly, the theory of everything is not a moral agent as it not only lacks sapience but also sentience and consciousness.

Evil can be easily explained within naturalism. The ToE is neither moral nor immoral. It is an amoral entity. Therefore, there is no problem of evil.

Modal realism

My main argument says that the ToE must exist in physical reality. Now, it follows that all possible worlds are governed by the ToE. For example, if string theory is the ToE, then all possible worlds are governed by it and there is no possible world which is governed by a different theory.

Modal realism is an argument that the idea of possible worlds is indispensable for philosophy and therefore the possible worlds must exist. This is very much like the Quine–Putnam indispensability argument which argues for the existence of the mathematical Platonic realm based on its indispensability to science. In our context since only worlds governed by string/M-theory are possible worlds it means that the set of possible worlds and the set of actual worlds both coincide with the string theory landscape.

Swampland (physics) is the set of (apparently) consistent effective field theories that cannot be UV completed into quantum gravity. Similarly, we can define Swampland (philosophy) as the set of (naively) consistent-looking possible worlds that are not actually consistent. The former Swampland is contained in the latter. Everything outside of the string theory landscape is contained in Swampland (philosophy), including theism, non-theistic supernatural religions that are compatible with atheism like Buddhism & Jainism, pseudoscience, nonreligious supernatural beliefs, etc. Everything outside naturalism (like religions, magic, etc) is contained within Swampland (philosophy). All of Swampland (physics) is contained within naturalism.

Rigour

The biggest problem with my argument is that I haven’t given a rigorous argument like Gödel’s ontological argument. I think it will be impatient to try to make a rigorous argument already. It will be better to make a rigorous argument after the problem of quantum gravity is settled and fundamental physics is over. Unfortunately, it might take a very long time, like centuries, for that to happen. If I am still existing in some form (like digitally) at that time, I will try to write a sequel to this post.

Criticism by Graham Oppy and my reply

I asked Graham Oppy, who is the biggest authority when it comes to ontological arguments, to provide any constructive criticism on this post so that I can improve it. He has kindly shared his criticism in an email. I will elaborate on my reply here.

1) Mathematical Platonism: He was skeptical about Mathematical Platonism. I already argued that mathematical beauty is evidence for Mathematical Platonism because this pure form of beauty is not man-made. Example: zoom video of the Mandelbrot set. As this argument doesn’t use any empirical data, within rationalism, you can use this argument for the existence of Mathematical Platonic realm and then deduce the physical world using the ontological argument and then predict scientific phenomena. So, everything can be reduced to reason. But I am neither a rationalist nor an empiricist. I certainly have more respect for rationalism than empiricism. The foundations of empiricism are too weak in front of philosophical skepticism. Science assumes many things like 1) consistency of important mathematical theories like ZFC set theory, etc, which can never be proved because of Gödel’s 2nd incompleteness theorem, 2) validity of the scientific method, 3) methodological naturalism, 4) induction (even Popper’s falsifiability doesn’t completely remove the need for induction and the problem of induction remains unsolved). Though from a rationalist point of view, my post only assumes 1) and tries to reduce everything to that; I think even rationalism is too weak in front of philosophical skepticism. I am an anti-foundationalist. I think epistemology will be more powerful if we use reason, empirical data, etc, together as the foundation. See Neurath’s boat; you can’t even just make the boat from scratch by swimming because philosophical skepticism is like a shark that will eat you if you enter the water. So, it’s better not to have a single foundation. The mathematical beauty alone is not a powerful enough argument for Mathematical Platonism, but when we couple it with the even stronger Quine–Putnam indispensability argument (1,2,3) I think it is more than enough justification for Mathematical Platonism. The main difference is that, unlike the previous argument, the Quine–Putnam indispensability argument assumes the physical world’s existence. So, I abandoned both rationalism and empiricism and embraced anti-foundationalism. From Gödel to Penrose, Connes etc many great people believed in Mathematical Platonism. Mathematical Realists like Albert Einstein, Henri Poincaré, G. H. Hardy, Charles Hermite etc were also probably Platonists. I do belive in it but in the next point I will assume it is wrong.

2) Without Mathematical Platonism: Even if Mathematical Platonism is wrong, I think my argument can be slightly modified and it will be compatible with most philosophies of mathematics. For example, if you believe in Mathematical Structuralism I can change my argument to “the existence of the greatest mathematical structure is logically necessary”. Similarly, Formalism, Logicism, etc are also compatible. I can broadly make the argument agnostic to any particular philosophy of mathematics by replacing “Mathematical Platonic Realm” with “Mathematical Entities” i.e., the greatest entity among Mathematical Entities. This loose version of the argument will be valid for most philosophies of mathematics except those like Intuitionism, etc., but these philosophies are IMO nonsense because if Maths was not there before any sapient beings like humans were created, how were there mathematical laws of physics before the birth of the first sapient being? This is similar nonsense like the Von Neumann–Wigner interpretation; of course, even before conscious beings were born, quantum phenomena were going on.

3) Defining greatness: He was telling me I haven’t defined greatness precisely. I agree that this is unsatisfactory. But, I have given many examples for comparing theories to give a rough picture. It would be nice if there is a precise algorithm that compares any given arbitrary theories and tells which is greater or if they both are euqally great.

4) Impossibility of physical existence of a mathematical entity: He said, “it is plausible that, if there are platonic entities, it is simply impossible for them to exist in physical reality.” In my opinion, we already know that laws of physics exist at each point in spacetime and “govern” all physical phenomena. So, the laws of physics is a unique example where it is both a mathematical entity but still exists in the physical world.

5) Causality: He thought it is “odd” to say that laws of physics “govern” the physical phenomena and “we might think that physical laws are just summaries of regularities”. He was telling laws of physics can’t cause anything. That is true, but causality itself is less fundamental than laws of physics. Whether an event can be caused by another event is dictated by the laws of physics. An event (point in spacetime) can only be caused by events in its past light cone, and it can only cause events in its future light cone (“can” but these causal relations are not necessary). When gravity is weak, the causal structure is trivial (i.e., light cones are always at 45 degrees). But near black holes, they bend significantly, and inside the event horizon, the time direction and radial direction both switch. It is the laws of physics that makes causality to be trivial when gravity is weak but weird near black holes.

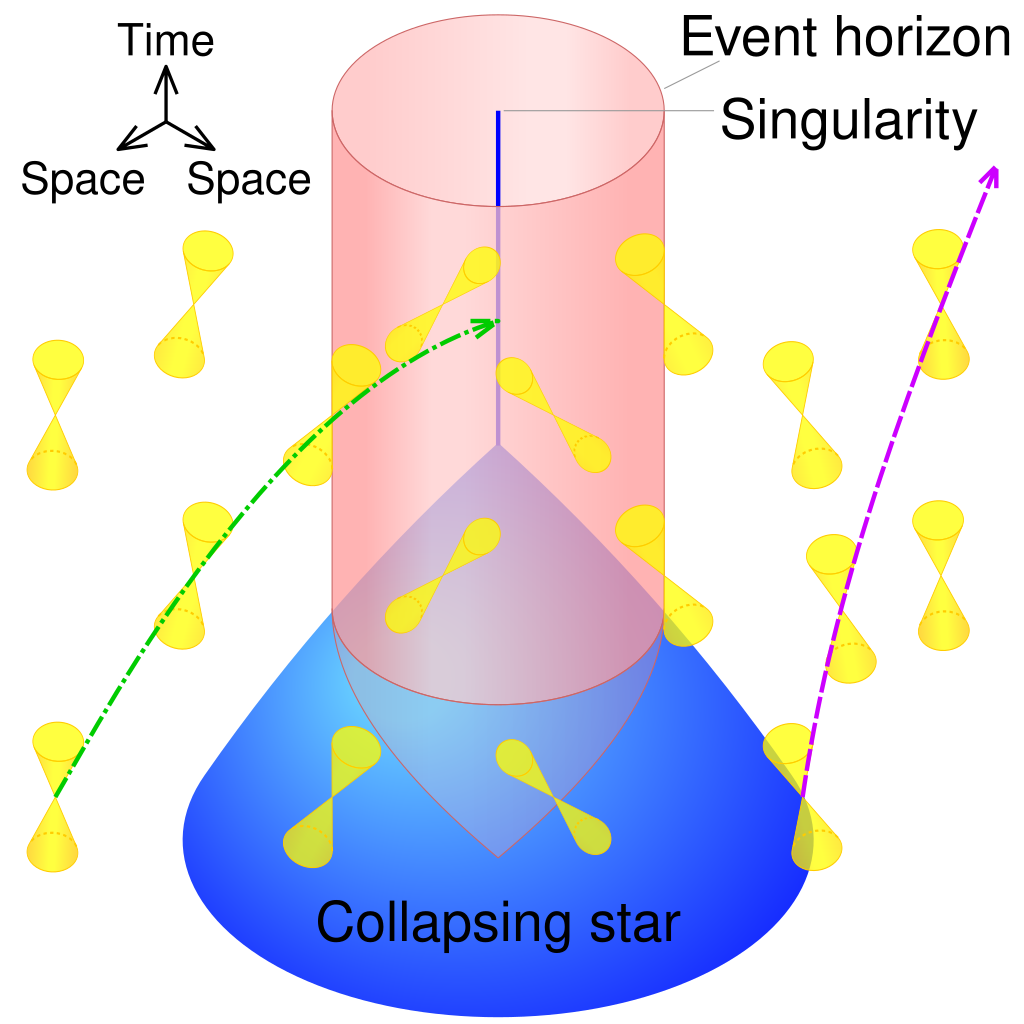
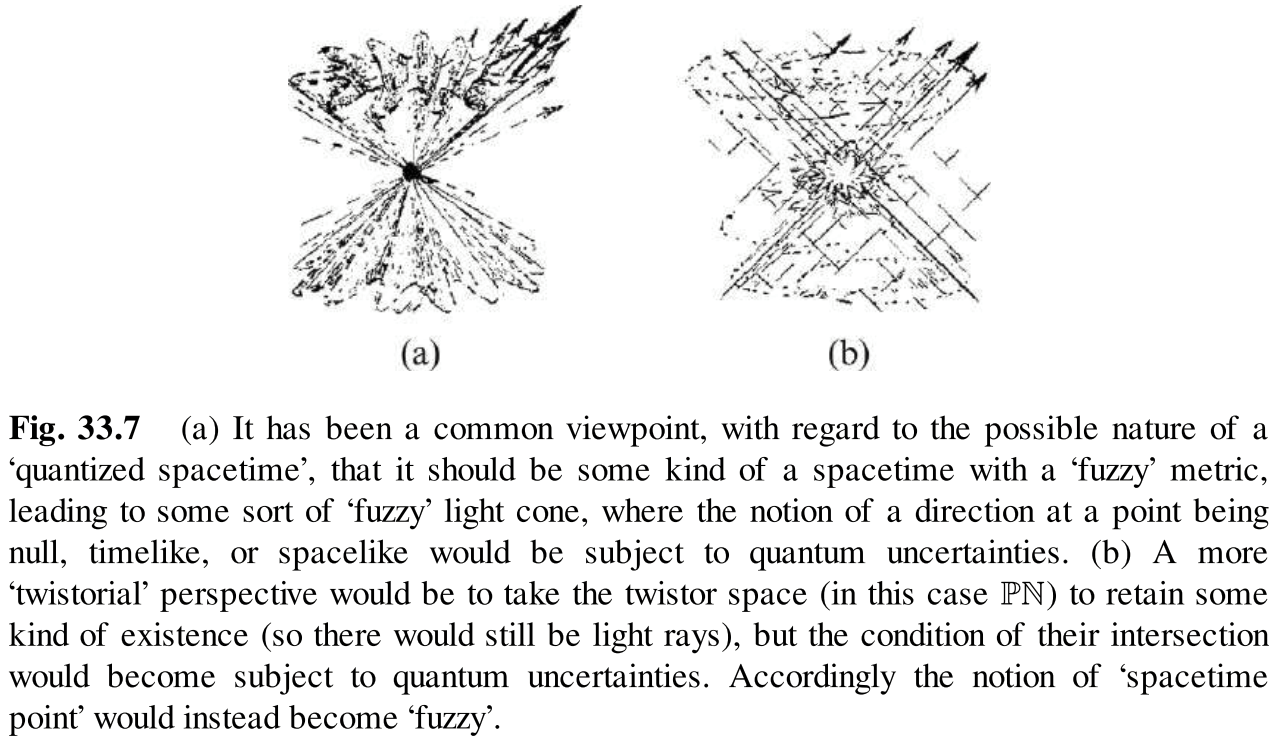
This is all in (the empirically established) general relativity. Quantum gravity is not yet understood, but the causal structure of quantum gravity will be even weirder. I wouldn’t be surprised if weird things like Retrocausality happen at the Planck scale. The below picture from The Road to Reality compares the causal structure of quantum gravity theories. Many proposed quantum gravity theories have fuzzy light cones like (a), but Penrose’s Twistor theory has (b). So, since causality itself depends on a specific quantum gravity theory, I think it is appropriate to say that the laws of physics “govern” physical phenomena.

Random note: For W. L. Craig’s Kalam cosmological argument, an objection that I have never seen is that he is applying a version of causality that is invalid at the initial singularity. When we are somewhat far from singularities, the quantum gravity fluctuations in light cones will be small and are described by the effective field theory approaximation of quantum gravity (arXiv:2106.05912). But, as we go near singularities (order of Planck length ($1.6\times 10^{-35}m$) from black hole singularities or order of Planck time ($5.4\times 10^{-44}s$) from initial singularities), these fluctuations increase and depend on a particlaur quantum gravity theory. Calculations near the singularities have not yet been done in any of the proposed theories. The causal structure at the Planck scale might be much weirder than we currently expect. So, Craig’s premises are unfounded.

Conclusion

“There is greater mathematics in Nature, Horatio, than is dreamt of in your Mathematics department.”

― Hamlet (if he was a pantheist)

I hope you are convinced that the ontological argument is not talking about some supernatural conscious entity, but it is actually telling us that the necessary entity is nothing but the fundamental law of physics. In the previous section, I even explained that this argument works without Mathematical Platonism.

Of course, for every philosophical claim, there will be reasonable, rational people who will object to it. So, I know many people might not be convinced by this blog post.

“Skepticism, while logically impeccable, is psychologically impossible, and there is an element of frivolous insincerity in any philosophy which pretends to accept it.”

“Is there any knowledge in the world which is so certain that no reasonable man could doubt it?” [The first line from The Problems of Philosophy. The answer is most probably no. If I haven’t included most probably, that sentence itself will become some knowledge.]

― Bertrand Russell

“The chief objection I have to Pantheism is that it says nothing. To call the world “God” is not to explain it; it is only to enrich our language with a superfluous synonym for the word “world”.”

― Arthur Schopenhauer

Years ago, like Schopenhauer, I thought Pantheism was nonsense, just like religions. As I said above, using the word “God” for the laws of physics will only tarnish the greatness of the laws of physics. In 2022, I understood that this semantic preference is not an argument against Pantheism and became a Pantheist. In the below Another Day of Thanking God meme, I replaced the G-word.

I used to think that fundamental physics was the most important because it is the most fundamental. But mathematics and philosophy are even more fundamental. And metaphilosophy and metamathematics are even more fundamental. And there are also meta-meta-mathematics and so on with more “meta”s. But this recognition did not decrease the importance of fundamental physics for me because now I think (like the G-word, I don’t like to use the exact religious terminology) doing fundamental physics is something akin to a rational form of “worship”.